LEC: 8 TOWARDS QUANTUM MECHANICAL MODEL OF THE ATOM
In view
of the shortcoming of the Bohr’s model, attempts were made to develop a more
suitable and general model for atoms. Two important developments which
contributed significantly in the formulation of such a model were :
1. Dual behaviour of matter,
2. Heisenberg uncertainty principle.
1. Dual behaviour of matter,
2. Heisenberg uncertainty principle.
Dual Behaviour of Matter
The
French physicist, de Broglie in 1924 proposed that matter, like radiation,
should also exhibit dual behaviour i.e., both particle and wavelike properties.
This means that just as the photon has momentum as well as wavelength,
electrons should also have momentum as well as wavelength, de Broglie gave the
following relation between wavelength (λ) and momentum (p) of a material
particle.
λ = h/mv =h/p
where m is the mass of the particle, v its velocity and p its momentum. de Broglie’s prediction was confirmed experimentally when it was found that an electron beam undergoes diffraction, a phenomenon characteristic of waves. The wavelengths associated with ordinary objects are so short (because of their large masses) that their wave properties cannot be detected. The wavelengths associated with electrons and other subatomic particles (with very small mass) can however be detected experimentally. Results obtained from the following problems prove these points qualitatively.
λ = h/mv =h/p
where m is the mass of the particle, v its velocity and p its momentum. de Broglie’s prediction was confirmed experimentally when it was found that an electron beam undergoes diffraction, a phenomenon characteristic of waves. The wavelengths associated with ordinary objects are so short (because of their large masses) that their wave properties cannot be detected. The wavelengths associated with electrons and other subatomic particles (with very small mass) can however be detected experimentally. Results obtained from the following problems prove these points qualitatively.
Heisenberg’s Uncertainty Principle
Werner Heisenberg a German physicist in 1927, stated uncertainty principle which is the consequence of dual behaviour of matter and radiation. It states that it is impossible to determine simultaneously, the exact position and exact momentum (or velocity) of an electron. Mathematically, it can be given as in equation
where Δx is the uncertainty in position and Δp ( or Δv) is the uncertainty in
momentum (or velocity) of the particle. If the position of the electron is
known with high degree of accuracy (Δx is small), then the velocity of the
electron will be uncertain (Δv is large). On the other hand, if the velocity of
the electron is known precisely (Δv is small), then the position of the
electron will be uncertain (Δx will be large).
now there must be some confusions and some question arises in our minds that are as follow:
Question1: What are difficulties in measurement of the position
and velocity?
Answer: in order to determine the position of an electron, we must use a
meterstick calibrated in units of smaller than the dimensions of electron (keep
in mind that an electron is considered as a point charge and is therefore,
dimensionless). To observe an electron, we can illuminate it with ‘light’ or
electromagnetic radiation. The ‘light’ used must have a wavelength smaller than
the dimensions of an electron. The high momentum photons of such light (p = h/
λ) would change the energy of electrons by collisions. In this process we, no
doubt, would be able to calculate the position of the electron, but we would
know very little about the velocity of the electron after the collision.
Question 2: what is Significance of Heisenberg’s Uncertainty Principle?
Answer: One of the important implications of the Heisenberg Uncertainty Principle is that it rules out existence of
definite paths or trajectories of electrons and other similar particles. The trajectory of an object is
determined by its location and velocity at various moments. If we know where a body is at a
particular instant and if we also know its velocity and the forces acting on it
at that instant, we can tell where the body would be sometime later. We,
therefore, conclude that the position of an object and its velocity fix its
trajectory. Since for a sub-atomic object such as an electron, it is not
possible simultaneously to determine the position and velocity at any given
instant to an arbitrary degree of precision, it is not possible to talk of the
trajectory of an electron.
Question 3: on which
particles Uncertainity priciple is
applicable?
Answer: The effect of Heisenberg Uncertainty Principle is significant
only for motion of microscopic objects and is negligible for that of
macroscopic objects. This can be seen from the following examples.
If uncertainty principle
is applied to an macroscopic object of mass10-6 kg, then
Δv.Δx = h/4π.m = (6.626×10-34)Js)/(4×3.1416×10-6 kg)
≈ 10-28m2s-1
The
value of ΔvΔx obtained is extremely small and is insignificant. Therefore, one
may say that in dealing with milligram-sized or heavier objects, the associated
uncertainties are hardly of any real consequence.
In the other case of a
microscopic object like an electron of mass is 9.11×10-31 kg, then
Δv.Δx = h/4π.m = (6.626×10-34)Js)/(4×3.1416×9.11×10-31 kg) = 10-4m2s-1
Δv.Δx = h/4π.m = (6.626×10-34)Js)/(4×3.1416×9.11×10-31 kg) = 10-4m2s-1
means that if we try to
find the exact location of the electron to an uncertainty of only 10-8 m,
then the uncertainty in Δv velocity
would be 10-4m2s-1/10-8m ≈ 104m s-1 which is so large that the classical picture of
electrons moving in Bohr’s orbits (fixed) cannot hold good.
RESULT: It, therefore, means that the precise statements of the
position and momentum of electrons have to be replaced by the statements of
probability, that the electron has at a given position and momentum. This is
what happens in the quantum mechanical model of atom.
QUANTUM MECHANICAL MODEL OF ATOM
Classical
mechanics, based on Newton’s laws of motion, successfully describes the motion
of all macroscopic objects such as a falling stone, orbiting planets etc.,
which have essentially a particle-like behavior as shown in the previous
section. However
it fails when applied to microscopic
objects like electrons, atoms, molecules etc. This is mainly because of the
fact that classical mechanics ignores the concept of dual behavior of matter
especially for sub-atomic particles and the uncertainty principle. The branch
of science that takes into account this dual behavior of matter is called quantum
mechanics. .
Quantum mechanics is a theoretical
science that deals with the study of the motions of the microscopic objects
that have both observable wave like and particle like properties. It specifies the laws of motion that these
objects obey. When quantum mechanics is applied to macroscopic objects (for
which wave like properties are insignificant) the results are the same as those
from the classical mechanics.
Quantum
mechanics was developed independently in 1926 by Werner Heisenberg and Erwin
Schrödinger. Here, however, we shall be discussing the quantum mechanics which
is based on the ideas of wave motion. The fundamental equation of quantum
mechanics was developed by Schrödinger and it won him the Nobel Prize in
Physics in 1933. Schrodinger equation is the
quantistical equivalent of Newton's law in the sense that while Newton's law
tells you the "future story" of a non-quantistical particle (its
trajectory due to forces), the Schrodinger equation tells you the same for a
quantistical particle. The difference being that for a quantistical particle
you cannot speak of a trajectory in the classical sense due to the Heisenberg
uncertainty principle, but you can speak of a wave function (with a
probabilistic meaning) and Schrodinger equation will tell you the "future
story" of the wave function
The total energy of the system takes into account the kinetic energies of all the sub-atomic particles (electrons, nuclei), attractive potential between the electrons and nuclei and repulsive potential among the electrons and nuclei individually. Solution of this equation gives E and ψ.
For a system (such as an atom or a
molecule whose energy does not change with time) the Schrödinger equation is
written as
The total energy of the system takes into account the kinetic energies of all the sub-atomic particles (electrons, nuclei), attractive potential between the electrons and nuclei and repulsive potential among the electrons and nuclei individually. Solution of this equation gives E and ψ.
Hydrogen Atom and the Schrödinger Equation
1) When Schrödinger equation is
solved for hydrogen atom, the solution gives the possible energy levels the
electron can occupy and the corresponding wave function(s) (ψ) of the electron
associated with each energy level.
2) When an electron is in any energy
state, the wave function corresponding to that energy state contains all
information about the electron.
3) Wave functions of hydrogen or
hydrogen like species with one electron are called atomic orbitals. Such wave
functions applicable to one-electron species are called one-electron systems.
4) The probability of finding an
electron at a point within an atom is proportional to the |ψ|2 at that point.
5) The quantum mechanical results of
the hydrogen atom successfully predict all aspects of the hydrogen atom
spectrum including some phenomena that could not be explained by the Bohr
model.
6) Application of Schrödinger equation to
multi-electron atoms presents a difficulty: the Schrödinger equation cannot be
solved exactly for a multi-electron atom. This difficulty can be overcome by
using approximate methods or by modern Computers.
Important Features of the Quantum Mechanical Model of Atom
Quantum
mechanical model of atom is the picture of the structure of the atom, which
emerges from the application of the Schrödinger equation to atoms. The
following are the important features of the quantum mechanical model of atom:
1) The energy of electrons in atoms is quantized means can only have
certain specific values.
2) The existence of quantized electronic energy levels is a direct solutions
of Schrödinger wave equation.
3) Both the exact position and exact velocity of an electron in an atom
cannot be determined simultaneously (Heisenberg uncertainty principle). The
path of an electron in an atom therefore, can never be determined or known
accurately. That is why, we can only talk about the probability of finding electron at different points in an atom.
4) A wave function for an electron in an atom is called an atomic
orbital. Whenever an electron is described by a wave function, we say that the
electron occupies that orbital.
Since many such wave functions (atomic orbital) are possible for an electron, In each orbital, the electron has a definite energy. All the information about the electron in an atom is stored in its orbital wave function ψ and quantum mechanics makes it possible to extract this information out of ψ.
Since many such wave functions (atomic orbital) are possible for an electron, In each orbital, the electron has a definite energy. All the information about the electron in an atom is stored in its orbital wave function ψ and quantum mechanics makes it possible to extract this information out of ψ.
5) The probability of finding an electron at a
point within an atom is proportional to the square of the orbital wave function
i.e., |ψ|2 at that point. |ψ|2 is
known as probability density and is always positive. From the value of |ψ|2 at different points within an atom, it is
possible to predict the region around the nucleus where electron will most
probably be found.
Orbitals and Quantum Numbers
We have already studied that by solving the
Schrödinger equation (Hψ = Eψ), we obtain a set of mathematical equations,
called wave functions (ψ), which describe the probability of finding electrons
at certain energy levels within an atom.
A wave function for an electron in an atom is
called an atomic orbital; this atomic
orbital describes a region of space in which there is a high probability of
finding the electron. Energy changes within an atom are the result of an
electron changing from a wave pattern with one energy to a wave pattern with a
different energy (usually accompanied by the absorption or emission of a photon
of light).
These quantized energy states and corresponding wave functions
which are characterized by a set of three quantum numbers principal quantum number n, azimuthal quantum number l and magnetic quantum number ml) arise in the solution of the Schrödinger equation. When an
electron is in any energy state, the wave function corresponding to that energy
state contains all information about the electron. The wave function is a
mathematical function whose value depends upon the coordinates of the electron
in the atom and does not carry any physical meaning.
Hence Each electron in an atom is described by four
different quantum numbers. The first three (n, l, ml) specify the particular
orbital of interest, and the fourth (ms) specifies how many electrons can
occupy that orbital. Now lets see all these quantum number in detail
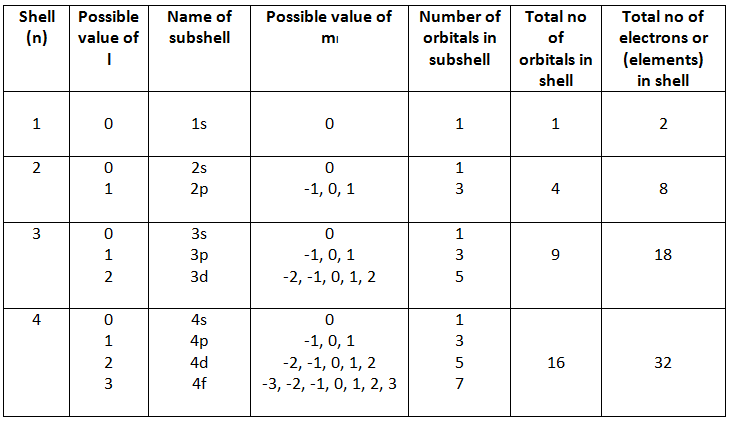
1) Principal Quantum Number (n):
a) Specifies the energy of an electron and the size of
the orbital (the distance from the nucleus), the larger the number n is, the farther the electrons are from the nucleus, the larger the size of the orbital, and the larger the atom is.
.
b) n can be any positive integer starting at 1, as n=1 designates the first principal shell (the innermost shell). The first principal shell is also called the ground state, or lowest energy state. All orbitals that have the same value of n are said to be in the same shell (level).
c) When an electron is in an excited state or it gains energy, it may jump to the second principle shell, where n=2. This is called absorption because the electron is "absorbing" photons, or energy. Known as emission, electrons can also "emit" energy as they jump to lower principle shells, where n decreases by whole numbers.
d) With the increase in the value of ‘n’, the number of allowed orbital increases and are given by ‘n2’.
e) All the orbitals of a given value of ‘n’ constitute a single shell of atom and are represented by the following letters
.
b) n can be any positive integer starting at 1, as n=1 designates the first principal shell (the innermost shell). The first principal shell is also called the ground state, or lowest energy state. All orbitals that have the same value of n are said to be in the same shell (level).
c) When an electron is in an excited state or it gains energy, it may jump to the second principle shell, where n=2. This is called absorption because the electron is "absorbing" photons, or energy. Known as emission, electrons can also "emit" energy as they jump to lower principle shells, where n decreases by whole numbers.
d) With the increase in the value of ‘n’, the number of allowed orbital increases and are given by ‘n2’.
e) All the orbitals of a given value of ‘n’ constitute a single shell of atom and are represented by the following letters
n = 1 2 3 4 ............
Shell = K L M N ............
When the value of n is higher, the number of principal electronic shells is greater. This causes a greater distance between the farthest electron and the nucleus. As a result, the size of the atom and its atomic radius increases.
c) Each sub-shell is assigned an azimuthal quantum number (l ). Sub-shells corresponding to different values of l are represented by the following symbols
When the value of n is higher, the number of principal electronic shells is greater. This causes a greater distance between the farthest electron and the nucleus. As a result, the size of the atom and its atomic radius increases.
2) Angular Momentum (Secondary / Azimunthal) Quantum Number (l)
a) it Specifies the shape of an orbital with a particular
principal quantum number.
b) Each shell consists of one or more subshells or sub-levels. The number of subshells in a principal shell is equal to the value of n from 0 to n-1.
b) Each shell consists of one or more subshells or sub-levels. The number of subshells in a principal shell is equal to the value of n from 0 to n-1.
c) Each sub-shell is assigned an azimuthal quantum number (l ). Sub-shells corresponding to different values of l are represented by the following symbols
value of l 0 1 2 3 4 5 ...
Name of Subshell s p d f g h ...
the arrangement can be shown as
3) Magnetic orbital quantum number. ‘ml’
a) The magnetic quantum number ml determines the number of orbitals and their orientation within a subshell.
b) its value depends on the orbital angular momentum quantum number l, For any sub-shell (defined by ‘l’ value) 2l+1 number of values of ml are possible and these values are given by
ml = -l, -(l-1), -(l-2)....-1, 0, 1, ....(l-2), (l-1), l
c) hence for a value of ml or subshell we can represent ml and number of orbital as
4) Electron Spin Quantum Number (ms)
The three quantum numbers labelling an atomic orbital can be used equally well to define its energy, shape and orientation. But all these quantum numbers are not enough to explain the line spectra observed in the case of multi-electron atoms, that is, some of the lines actually occur in doublets (two lines closely spaced), triplets (three lines, closely spaced) etc. This suggests the presence of a few more energy levels than predicted by the three quantum numbers.
In 1925, George Uhlenbeck and Samuel Goudsmit proposed the presence of the fourth quantum number known as the electron spin quantum number (ms). An electron spins around its own axis, much in a similar way as earth spins around its own axis while revolving around the sun. In other words, an electron has, besides charge and mass, intrinsic spin angular quantum number. Spin angular momentum of the electron — a vector quantity, can have two orientations relative to the chosen axis. These two orientations are distinguished by the spin quantum numbers ms which can take the values of +½ or –½. These are called the two spin states of the electron and are normally represented by two arrows, ↑ (spin up) and ↓ (spin down). Two electrons that have different ms values (one +½ and the other –½) are said to have opposite spins. An orbital cannot hold more than two electrons and these two electrons should have opposite spins.





No comments:
Post a Comment