UNIT 2.5 ATOMIC STRUCTURE - SHAPES AND FILLING OF ORBITALS IN ATOM

LEC 9  Shapes of Atomic Orbitals

The orbital wave function or ψ for an electron in an atom has no physical meaning. It is simply a mathematical function of the coordinates of the electron but the square of the wave function (i.e.,ψ²) at a point gives the probability density of the electron at that point.
An orbitals is the region of space around the nucleus within which the probability of finding an electron of given energy is maximum above 90%. the shape of this region (electron cloud) gives the shape of the orbital that determine by the azimuthal quantum number (l) while the orientation of the orbitals depends on the magnetic quantum number (m). lets now see the shape of orbitals in the various subshells.

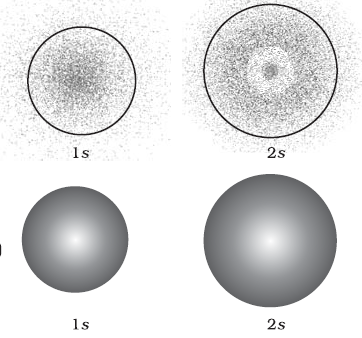
1) S-Orbitals (l=0)

The variation of ψ² as a function of r for 1s and 2s orbitals is given as

It may be noted that 

1) for 1s orbital the probability density is maximum at the nucleus and it decreases sharply as we move away from it. On the other hand, for 2s orbital the probability density first decreases sharply to zero and again starts increasing. After reaching a small maxima it decreases again and approaches zero as the value of r increases further. The region where this probability density function reduces to zero is called nodal surfaces or simply nodes. In general,

2) it has been found that ns-orbital has (n – 1) nodes, that is, number of nodes increases with increase of principal quantum number n. In other words, number of nodes for 2s orbital is one, two for 3s and so on but there is no nodes for 1s orbitals.

3) boundry surface diagram of constant probability density for different orbitals give a fairly good representation of the shapes of the orbitals. In this representation, a boundary surface or contour surface is drawn in space for an orbital on which the value of probability density |ψ|² is constant or more than 90%.

4) we see that 1s and 2s orbitals are spherically symmetric, that is, the probability of finding the electron at a given distance is equal in all the directions. It is also observed that the size of the s orbital increases with increase in n, that is, 4s > 3s > 2s > 1s and the electron is located further away from the nucleus as the principal quantum number increases.

 2) P-orbitals (l=1)

1) unlike s-orbitals, the boundary surface diagrams are not spherical. Instead each p orbital consists of two sections called lobes that are on either side of the plane that passes through the nucleus. The probability density function is zero on the plane where the two lobes touch each other.

2) for l=1 the value of m is three that is -1, 0, 1 so P orbitals have three different orientation and they are given the designations 2p_x, 2p_y, and 2p_z  as lobes may be considered to lie along the x, y or z axis.

3) p orbitals increase in size and energy with increase in the principal quantum number and hence the order of the energy and size of various p orbitals is 4p > 3p > 2p.

4) the probability density functions for p-orbital also pass through value zero, besides at zero and infinite distance, as the distance from the nucleus increases. The number of radial nodes are given by the n-–2, that is number of radial node is 1 for 3p orbital, two for 4p orbital and so on, while l gives angular node that is 1 in case all of p orbitals means total nodes in 3p orbitals are 2 and in 4 p orbitals 3.

3) d-orbitals (l=2)

1) They have relatively complex geometry for l=2 we have five value of m that is -2, -1, 0, 1, 2 means d orbitals have 5 different orientation and they are given designation as

2) The shapes of the first four d-orbitals are similar to each other, where as that of the fifth one, dz² is different from others. all five 3d orbitals are equivalent in energy. The d orbitals for which n is greater than 3 (4d, 5d…) also have shapes similar to 3d orbital, but differ in energy and size.

Radial and Angular Nodes

There are two types of nodes that can occur; angular and radial nodes. An angular node is a flat plane, The ℓ quantum number determines the number of angular nodes an orbital will have. A radial node is a circular ring that occurs as the principle quantum number increases. Thus, n tells us how many radial nodes an orbital will have and is calculable with the equation: 

Total Number of Nodes = n-1.

Number of Angular Nodes = l.

Number of radial Nodes = Total Nodes - Angular Nodes   

For example, let us determine the nodes in the 3pz orbital. We are given that n = 3 and ℓ = 1 because of the p orbital. We can determine the total number of nodes present in this orbital because: nodes = n-1. In this case, 3-1=2, so there is a total of 2 nodes. The quantum number ℓ tells us how many angular nodes there are, so there is 1 angular node, specifically on the xy plane because this is a pz orbital. Since there is one node left, there must be one radial node. To sum up, the 3pz orbital has 2 nodes: 1 angular node and 1 radial node.

Energies of Orbitals

For example, energy of 2s orbital of hydrogen atom is greater than that of 2s orbital of lithium.

1) The energy of an electron in a hydrogen atom is determined solely by the principal quantum number. Thus the energy of the orbitals increases as follows :

1s < 2s = 2p < 3s = 3p = 3d < 4s = 4p = 4d = 4f < 

The shapes of 2s and 2p orbitals are different, an electron has the same energy when it is in the 2s orbital as when it is present in 2p orbital. The orbitals having the same energy are called degenerate.

2) The energy of an electron in a multielectron atom, unlike that of the hydrogen atom, depends not only on its principal quantum number (shell), but also on its azimuthal quantum number (subshell). That is, for a given principal quantum number, s, p, d, f … all have different energies.

The main reason for having different energies of the subshells is the mutual repulsion among the electrons in a multi-electron atoms. The only electrical interaction present in hydrogen atom is the attraction between the negatively charged electron and the positively charged nucleus. In multi-electron atoms, besides the presence of attraction between the electron and nucleus, there are repulsion terms between every electron and other electrons present in the atom. Thus the stability of an electron in multi-electron atom is because total attractive interactions are more than the repulsive interactions.

3) On the other hand, the attractive interactions of an electron increases with increase of positive charge (Ze) on the nucleus. the energy of interaction between, the nucleus and electron (that is orbital energy) decreases (that is more negative) with the increase of atomic number (Z). Hence that energies of the orbitals in the same subshell decrease with increase in the atomic number (Z_eff ).

4)  Both the attractive and repulsive interactions depend upon the shell and shape of the orbital in which the electron is present. Further due to spherical shape, s orbital electron spends more time close to the nucleus in comparison to p orbital and p orbital spends more time in the vicinity of nucleus in comparison to d orbital. In other words, for a given shell (principal quantum number), the Z_eff experienced by the orbital decreases with increase of azimuthal.

5) The repulsive interaction of the electrons in the outer shell with the electrons in the inner shell are more important. . Due to the presence of electrons in the inner shells, the electron in the outer shell will not experience the full positive charge on the nucleus (Ze), but will be lowered due to the partial screening of positive charge on the nucleus by the inner shell electrons. This is known as the shielding of the outshell electrons from the nucleus by the inner shell electrons, and the net positive charge experienced by the electron from the nucleus is known as effective nuclear charge (Z_eff e).

The order of shielding effect is s>p>d>f means being spherical in shape, the s orbital shields the electrons from the nucleus more effectively as compared to p and d orbital, even though all these orbitals are present in the same shell.

6) Since the extent of shielding of the nucleus is different for different orbitals, it leads to the splitting of the energies of the orbitals within the same shell (or same principal quantum number), that is, energy of the orbital, as mentioned earlier, depends upon the values of n and l. Mathematically, the dependence of energies of the orbitals on n and l are quite complicated but one simple rule is that of combined value of n and l. The lower the value of (n + l) for an orbital, the lower is its energy. If two orbitals have the same value of (n + l), the orbital with lower value of n will have the lower energy.

It may be noted that different subshells of a particular shell have different energies in case of multi-electrons atoms. However, in hydrogen atom, these have the same energy.

Filling of Orbitals in Atom

The filling of electrons into the orbitals of different atoms takes place according to the aufbau principle which is based on the Pauli’s exclusion principle, the Hund’s rule of maximum multiplicity and the relative energies of the orbitals.

Aufbau Principle

The principle states : In the ground state of the atoms, the orbitals are filled in order of their increasing energies. In other words, electrons first occupy the lowest energy orbital available to them and enter into higher energy orbitals only after the lower energy orbitals are filled.

The order in which the energies of the orbitals increase and hence the order in which the orbitals are filled is as follows :

1s, 2s, 2p, 3s, 3p, 4s, 3d, 4p, 5s, 4d, 5p, 4f, 5d, 6p, 7s…

The order may be remembered by using the method given in the fig. Starting from the top, the direction of the arrows gives the order of filling of orbitals, that is starting from right top to bottom left

Pauli Exclusion Principle

The number of electrons to be filled in various orbitals is restricted by the pauli exclusion principle, According to this principle : No two electrons in an atom can have the same set of four quantum numbers. Pauli exclusion principle can also be stated as : “Only two electrons may exist in the same orbital and these electrons must have opposite spin.” This means that the two electrons can have the same value of three quantum numbers n, l and m_l, but must have the opposite spin quantum number. The restriction imposed by Pauli’s exclusion principle on the number of electrons in an orbital helps in calculating the capacity of electrons to be present in any subshell. For example, subshell 1s comprises of one orbital and thus the maximum number of electrons present in 1s subshell can be two, in p and d subshells, the maximum number of electrons can be 6 and 10 and so on. This can be summed up as : the maximum number of electrons in the shell with principal quantum number n is equal to 2n².

Hund’s Rule of Maximum Multiplicity

This rule deals with the filling of electrons into the orbitals belonging to the same subshell (that is, orbitals of equal energy, called degenerate orbitals). It states : pairing of electrons in the orbitals belonging to the same subshell (p, d or f) does not take place until each orbital belonging to that subshell has got one electron each i.e., it is singly occupied.

Since there are three p, five d and seven f orbitals, therefore, the pairing of electrons will start in the p, d and f orbitals with the entry of 4th, 6th and 8th electron, respectively. It has been observed that half filled and fully filled degenerate set of orbitals acquire extra stability due to their symmetry.

Stability of Completely Filled and Half Filled Subshells

The ground state electronic configuration of the atom of an element always corresponds to the state of the lowest total electronic energy. The electronic configurations of most of the atoms follow the basic rules, However, in certain elements such as Cu, or Cr, where the two subshells (4s and 3d) differ slightly in their energies, an electron shifts from a subshell of lower energy (4s) to a subshell of higher energy (3d), provided such a shift results in all orbitals of the subshell of higher energy getting either completely filled or half filled. The valence electronic configurations of Cr and Cu, therefore, are 3d⁵4s¹ and 3d¹⁰ 4s¹ respectively and not 3d⁴ 4s² and 3d⁹ 4s². It has been found that there is extra stability associated with these electronic configurations.

Stability of Completely Filled and Half Filled Subshells

The ground state electronic configuration of the atom of an element always corresponds to the state of the lowest total electronic energy. It has been found that there is extra stability associated with completely filled and half filled electronic configurations because of following reasons: 

1) Symmetrical distribution of electrons:

The completely filled or half filled subshells have symmetrical distribution of electrons in them and are therefore more stable. their shielding of one another is relatively small and the electrons are more strongly attracted by the nucleus.

2. Exchange Energy:

The stabilizing effect arises whenever two or more electrons with the same spin are present in the degenerate orbitals of a subshell. These electrons tend to exchange their positions and the energy released due to this exchange is called exchange energy. The number of exchanges that can take place is maximum when the subshell is either half filled or completely filled As a result the exchange energy is maximum and so is the stability.

We can say that  the extra stability of half-filled and completely filled subshell is due to:

1) relatively small shielding,

2) smaller coulombic repulsion energy, and

3) larger exchange energy.

Details about the exchange energy will be dealt with in higher classes.

Electronic Configuration of Atoms

The distribution of electrons into orbitals of an atom is called its electronic configuration. If one keeps in mind the basic rules which govern the filling of different atomic orbitals, the electronic configurations of different atoms can be written very easily.

The electronic configuration of different atoms can be represented in two ways : 

(i) s^a p^b d^c …… notation

(ii) Orbital diagram

In the first notation, the subshell is represented by the respective letter symbol and the number of electrons present in the subshell is depicted, as the super script, like a, b, c, … etc. The similar subshell represented for different shells is differentiated by writing the principal quantum number before the respective subshell.

In the second notation each orbital of the subshell is represented by a box and the electron is represented by an arrow (↑) a positive spin or an arrow (↓) a negative spin. The advantage of second notation over the first is that it represents all the four quantum numbers.

The electrons in the completely filled shells are known as core electrons and the electrons that are added to the  electronic shell with the highest principal quantum number are called valence electrons. For example, the electrons in Ne are the core electrons and the electrons from Na to Ar are the valence electrons.

We may be puzzled by the fact that chromium and copper have five and ten electrons in 3d orbitals rather than four and nine as their position would have indicated with two-electrons in the 4s orbital. The reason is p³, p⁶, d⁵, d¹⁰, f⁷, f¹⁴ are fully filled orbitals and halffilled orbitals have extra stability.

the electronic configuration is show as:

..........END OF THIS UNIT..........