Unit 1.1 THE SOLID STATE

lec 1  Introduction

We use solid in everyday life for different purpose for example alumunium wire for electrical purpose, wood for thermal insulator, metal rod for heat conduction, magnet for locate direction etc. For different Applications and purpose we need solids with widely different properties like electrical properties, thermal properties, optical properties etc.These properties depend upon the nature of constituent particles and the binding forces operating between them. Therefore, study of the structure of solids is important. The correlation between structure and properties helps in discovering new solid materials with desired properties like high temperature superconductors, magnetic materials, biodegradable polymers for packaging, biocompliant solids for surgical implants, etc.

From our earlier studies, we know that liquids and gases are called fluids because of their ability to flow. The fluidity in both of these states is due to the fact that the molecules are free to move about. On the other hand, the constituent particles in solids have fixed positions and can only oscillate about their mean positions. This explains the rigidity in solids. Under a given set of conditions of temperature and pressure, which of these would be the most stable state of a given substance depends upon the net effect of two opposing factors. Intermolecular forces tend to keep the molecules (or atoms or ions) closer, whereas thermal energy tends to keep them apart by making them move faster. At sufficiently low temperature, the thermal energy is low and intermolecular forces bring them so close that they cling to one another and occupy fixed positions. These can still oscillate about their mean positions and the substance exists in solid state.

The following are the characteristic properties of the solid state:

(i) They have definite mass, volume and shape.

(ii) Intermolecular distances are short.

(iii) Intermolecular forces are strong.

(iv) Their constituent particles (atoms, molecules or ions) have fixed positions and can only oscillate about their mean positions.

(v) They are incompressible and rigid.

Classification of solids

Solids can be classified as crystalline (true solid) and amorphous (Super condensed liquid) on the basis of the nature of order present in the arrangement of their constituent particles.

A crystalline solid usually consists of a large number of small crystals, each of them having a definite characteristic geometrical shape. In a crystal, the arrangement of constituent particles (atoms, molecules or ions) is ordered. It has long range order which means that there is a regular pattern of arrangement of particles which repeats itself periodically over the entire crystal. Sodium chloride and quartz are typical examples of crystalline solids. 

An amorphous solid (Greek amorphos = no form) consists of particles of irregular shape. The arrangement of constituent particles (atoms, molecules or ions) in such a solid has only short range order. In such an arrangement, a regular and periodically repeating pattern is observed over short distances only. Such portions are scattered and in between the arrangement is disordered. The structures of quartz (crystalline) and quartz glass (amorphous) are shown as

While the two structures are almost identical, yet in the case of amorphous quartz glass there is no long range order. The structure of amorphous solids is similar to that of liquids. Glass, rubber and plastics are typical examples of amorphous solids. Due to the differences in the arrangement of the constituent particles, the two types of solids differ in their properties as follow: 

Crystalline solids have a sharp melting point because As the atoms of Crystalline solids have specific shape and same distance,so they have same K.E, intermolecular forces of attraction and geometrical shape due to which bond strenght is same so start melting at fixed temprature.on the other hand, amorphous solids soften over a range of temperature it havent specefic shape so bond strenght are different in different point hence it start melting over a range of temprature.

On heating amorphous solid become crystalline at Some temperature, Amorphous solids contain short range crystal particle arrangement which get more mobility at higher temperature to rearrange itself in such a way that long range crystal particle arrangement is observed. In such condition amorphous solid become crystalline.

Glass panes fixed to windows or doors of old buildings are invariably found to be slightly thicker at the bottom than at the top. This is because the glass flows down very slowly and makes the bottom portion slightly thicker Like liquids, amorphous solids have a tendency to flow, though very slowly. Therefore, sometimes these are called pseudo solids or super cooled liquids.

Crystalline solids are anisotropic in nature, that is, some of their physical properties like electrical resistance or refractive index show different values when measured along different directions in the same crystals. This arises from different arrangement of particles in different directions. 

Anistropic

Amorphous solids on the other hand are isotropic in nature. It is because there is no long range order in them and arrangement is irregular along all the directions. Therefore, value of any physical property would be same along any direction.

Amorphous solids are useful materials. Glass, rubber and plastics find many applications in our daily lives. Amorphous silicon is one of the best photovoltaic material available for conversion of sunlight into electricity

most of the solid substances are crystalline in nature. For example, all the metallic elements like iron, copper and silver; non – metallic elements like sulphur, phosphorus and iodine and compounds like sodium chloride, zinc sulphide and naphthalene form crystalline solids.

Crystalline solids can be classified on the basis of nature of intermolecular forces operating in them into four categories:

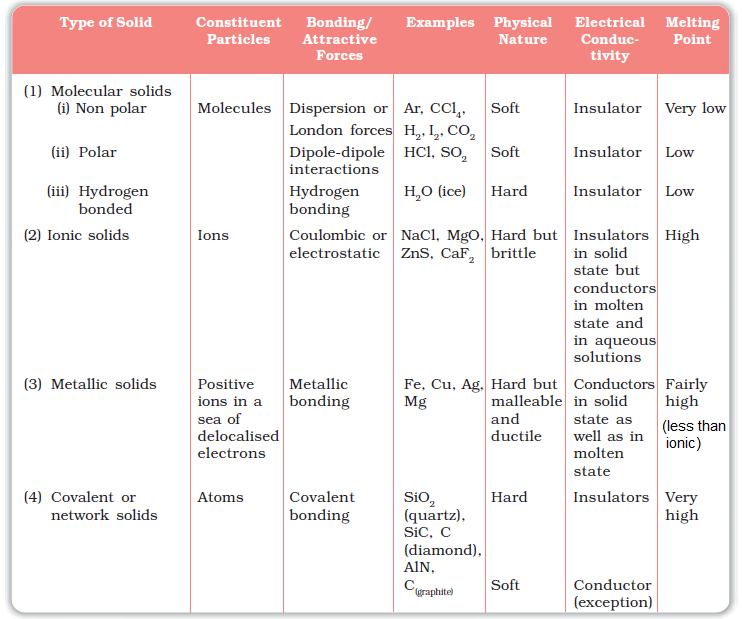
1) Molecular,

4) Ionic,

3) Metallic and

4) Covalent solids.

Let us now learn about these categories.

1) Molecular Solid 

Molecules are the constituent particles of molecular solids. These are further sub divided into the following categories:

(i) Non polar Molecular Solids:

They comprise of either atoms, for example, argon and helium or the molecules formed by non polar covalent bonds for example H2, Cl2 and I2. In these solids, the atoms or molecules are held by weak dispersion forces or London forces. These solids are soft and non-conductors of electricity. They have low melting points and are usually in liquid or gaseous state at room temperature and pressure.

(ii) Polar Molecular Solids:

The molecules of substances like HCl, SO2, etc. are formed by polar covalent bonds. The molecules in such solids are held together by relatively stronger dipole-dipole interactions. These solids are soft and non-conductors of electricity. Their melting points are higher than those of non polar molecular solids yet most of these are gases or liquids under room temperature and pressure. Solid SO2 and solid NH3 are some examples of such solids.

(iii) Hydrogen Bonded Molecular Solids:

The molecules of such solids contain polar covalent bonds between H and F, O or N atoms. Strong hydrogen bonding binds molecules of such solids like H2O (ice). They are non-conductors of electricity. Generally they are volatile liquids or soft solids under room temperature and pressure.

2) Ionic Solid

Ions are the constituent particles of ionic solids. Such solids are formed by the three dimensional arrangements of cations and anions bound by strong coulombic (electrostatic) forces. 

These solids are hard and brittle in nature. They have high melting and boiling points. Since the ions are not free to move about, they are electrical insulators in the solid state. However, in the molten state or when dissolved in water, the ions become free to move about and they conduct electricity.

3) Metallic Solid

Metals are orderly collection of positive ions surrounded by and held together by a sea of free electrons. These electrons are mobile and are evenly spread out throughout the crystal. Each metal atom contributes one or more electrons towards this sea of mobile electrons. These free and mobile electrons are responsible for high electrical and thermal conductivity of metals.

When an electric field is applied, these electrons flow through the network of positive ions. Similarly, when heat is supplied to one portion of a metal, the thermal energy is uniformly spread throughout by free electrons. Another important characteristic of metals is their lustre and colour in certain cases because of electrons passing freely between them which makes light bounce evenly and shine in that special metallic reflection. This is also due to the presence of free electrons in them. Metals are highly malleable (converted in sheet) and ductile (converted in wire).

4) Covalent Solid 

A wide variety of crystalline solids of non-metals result from the formation of covalent bonds between adjacent atoms throughout the crystal. Covalent bonds are strong and directional in nature, therefore atoms are held very strongly at their positions. Such solids are very hard and brittle. They have extremely high melting points and may even decompose before melting. They are insulators and do not conduct electricity. Diamond and silicon carbide are typical examples of such solids. 
Graphite is soft and  conductor of electricity. Its exceptional properties are due to its typical structure. Carbon atoms are arranged in different layers and each atom is covalently bonded to three of its neighbouring atoms in the same layer. The fourth valence electron of each atom is present between different layers and is free to move about. These free electrons make graphite a good conductor of electricity. Different layers can slide one over the other. This makes graphite a soft solid and a good solid lubricant

The different properties of the four types of solids are listed as

UNIT 2.5 ATOMIC STRUCTURE - SHAPES AND FILLING OF ORBITALS IN ATOM

LEC 9  Shapes of Atomic Orbitals

The orbital wave function or ψ for an electron in an atom has no physical meaning. It is simply a mathematical function of the coordinates of the electron but the square of the wave function (i.e.,ψ²) at a point gives the probability density of the electron at that point.
An orbitals is the region of space around the nucleus within which the probability of finding an electron of given energy is maximum above 90%. the shape of this region (electron cloud) gives the shape of the orbital that determine by the azimuthal quantum number (l) while the orientation of the orbitals depends on the magnetic quantum number (m). lets now see the shape of orbitals in the various subshells.

1) S-Orbitals (l=0)

The variation of ψ² as a function of r for 1s and 2s orbitals is given as

It may be noted that 

1) for 1s orbital the probability density is maximum at the nucleus and it decreases sharply as we move away from it. On the other hand, for 2s orbital the probability density first decreases sharply to zero and again starts increasing. After reaching a small maxima it decreases again and approaches zero as the value of r increases further. The region where this probability density function reduces to zero is called nodal surfaces or simply nodes. In general,

2) it has been found that ns-orbital has (n – 1) nodes, that is, number of nodes increases with increase of principal quantum number n. In other words, number of nodes for 2s orbital is one, two for 3s and so on but there is no nodes for 1s orbitals.

3) boundry surface diagram of constant probability density for different orbitals give a fairly good representation of the shapes of the orbitals. In this representation, a boundary surface or contour surface is drawn in space for an orbital on which the value of probability density |ψ|² is constant or more than 90%.

4) we see that 1s and 2s orbitals are spherically symmetric, that is, the probability of finding the electron at a given distance is equal in all the directions. It is also observed that the size of the s orbital increases with increase in n, that is, 4s > 3s > 2s > 1s and the electron is located further away from the nucleus as the principal quantum number increases.

 2) P-orbitals (l=1)

1) unlike s-orbitals, the boundary surface diagrams are not spherical. Instead each p orbital consists of two sections called lobes that are on either side of the plane that passes through the nucleus. The probability density function is zero on the plane where the two lobes touch each other.

2) for l=1 the value of m is three that is -1, 0, 1 so P orbitals have three different orientation and they are given the designations 2p_x, 2p_y, and 2p_z  as lobes may be considered to lie along the x, y or z axis.

3) p orbitals increase in size and energy with increase in the principal quantum number and hence the order of the energy and size of various p orbitals is 4p > 3p > 2p.

4) the probability density functions for p-orbital also pass through value zero, besides at zero and infinite distance, as the distance from the nucleus increases. The number of radial nodes are given by the n-–2, that is number of radial node is 1 for 3p orbital, two for 4p orbital and so on, while l gives angular node that is 1 in case all of p orbitals means total nodes in 3p orbitals are 2 and in 4 p orbitals 3.

3) d-orbitals (l=2)

1) They have relatively complex geometry for l=2 we have five value of m that is -2, -1, 0, 1, 2 means d orbitals have 5 different orientation and they are given designation as

2) The shapes of the first four d-orbitals are similar to each other, where as that of the fifth one, dz² is different from others. all five 3d orbitals are equivalent in energy. The d orbitals for which n is greater than 3 (4d, 5d…) also have shapes similar to 3d orbital, but differ in energy and size.

Radial and Angular Nodes

There are two types of nodes that can occur; angular and radial nodes. An angular node is a flat plane, The ℓ quantum number determines the number of angular nodes an orbital will have. A radial node is a circular ring that occurs as the principle quantum number increases. Thus, n tells us how many radial nodes an orbital will have and is calculable with the equation: 

Total Number of Nodes = n-1.

Number of Angular Nodes = l.

Number of radial Nodes = Total Nodes - Angular Nodes   

For example, let us determine the nodes in the 3pz orbital. We are given that n = 3 and ℓ = 1 because of the p orbital. We can determine the total number of nodes present in this orbital because: nodes = n-1. In this case, 3-1=2, so there is a total of 2 nodes. The quantum number ℓ tells us how many angular nodes there are, so there is 1 angular node, specifically on the xy plane because this is a pz orbital. Since there is one node left, there must be one radial node. To sum up, the 3pz orbital has 2 nodes: 1 angular node and 1 radial node.

Energies of Orbitals

For example, energy of 2s orbital of hydrogen atom is greater than that of 2s orbital of lithium.

1) The energy of an electron in a hydrogen atom is determined solely by the principal quantum number. Thus the energy of the orbitals increases as follows :

1s < 2s = 2p < 3s = 3p = 3d < 4s = 4p = 4d = 4f < 

The shapes of 2s and 2p orbitals are different, an electron has the same energy when it is in the 2s orbital as when it is present in 2p orbital. The orbitals having the same energy are called degenerate.

2) The energy of an electron in a multielectron atom, unlike that of the hydrogen atom, depends not only on its principal quantum number (shell), but also on its azimuthal quantum number (subshell). That is, for a given principal quantum number, s, p, d, f … all have different energies.

The main reason for having different energies of the subshells is the mutual repulsion among the electrons in a multi-electron atoms. The only electrical interaction present in hydrogen atom is the attraction between the negatively charged electron and the positively charged nucleus. In multi-electron atoms, besides the presence of attraction between the electron and nucleus, there are repulsion terms between every electron and other electrons present in the atom. Thus the stability of an electron in multi-electron atom is because total attractive interactions are more than the repulsive interactions.

3) On the other hand, the attractive interactions of an electron increases with increase of positive charge (Ze) on the nucleus. the energy of interaction between, the nucleus and electron (that is orbital energy) decreases (that is more negative) with the increase of atomic number (Z). Hence that energies of the orbitals in the same subshell decrease with increase in the atomic number (Z_eff ).

4)  Both the attractive and repulsive interactions depend upon the shell and shape of the orbital in which the electron is present. Further due to spherical shape, s orbital electron spends more time close to the nucleus in comparison to p orbital and p orbital spends more time in the vicinity of nucleus in comparison to d orbital. In other words, for a given shell (principal quantum number), the Z_eff experienced by the orbital decreases with increase of azimuthal.

5) The repulsive interaction of the electrons in the outer shell with the electrons in the inner shell are more important. . Due to the presence of electrons in the inner shells, the electron in the outer shell will not experience the full positive charge on the nucleus (Ze), but will be lowered due to the partial screening of positive charge on the nucleus by the inner shell electrons. This is known as the shielding of the outshell electrons from the nucleus by the inner shell electrons, and the net positive charge experienced by the electron from the nucleus is known as effective nuclear charge (Z_eff e).

The order of shielding effect is s>p>d>f means being spherical in shape, the s orbital shields the electrons from the nucleus more effectively as compared to p and d orbital, even though all these orbitals are present in the same shell.

6) Since the extent of shielding of the nucleus is different for different orbitals, it leads to the splitting of the energies of the orbitals within the same shell (or same principal quantum number), that is, energy of the orbital, as mentioned earlier, depends upon the values of n and l. Mathematically, the dependence of energies of the orbitals on n and l are quite complicated but one simple rule is that of combined value of n and l. The lower the value of (n + l) for an orbital, the lower is its energy. If two orbitals have the same value of (n + l), the orbital with lower value of n will have the lower energy.

It may be noted that different subshells of a particular shell have different energies in case of multi-electrons atoms. However, in hydrogen atom, these have the same energy.

Filling of Orbitals in Atom

The filling of electrons into the orbitals of different atoms takes place according to the aufbau principle which is based on the Pauli’s exclusion principle, the Hund’s rule of maximum multiplicity and the relative energies of the orbitals.

Aufbau Principle

The principle states : In the ground state of the atoms, the orbitals are filled in order of their increasing energies. In other words, electrons first occupy the lowest energy orbital available to them and enter into higher energy orbitals only after the lower energy orbitals are filled.

The order in which the energies of the orbitals increase and hence the order in which the orbitals are filled is as follows :

1s, 2s, 2p, 3s, 3p, 4s, 3d, 4p, 5s, 4d, 5p, 4f, 5d, 6p, 7s…

The order may be remembered by using the method given in the fig. Starting from the top, the direction of the arrows gives the order of filling of orbitals, that is starting from right top to bottom left

Pauli Exclusion Principle

The number of electrons to be filled in various orbitals is restricted by the pauli exclusion principle, According to this principle : No two electrons in an atom can have the same set of four quantum numbers. Pauli exclusion principle can also be stated as : “Only two electrons may exist in the same orbital and these electrons must have opposite spin.” This means that the two electrons can have the same value of three quantum numbers n, l and m_l, but must have the opposite spin quantum number. The restriction imposed by Pauli’s exclusion principle on the number of electrons in an orbital helps in calculating the capacity of electrons to be present in any subshell. For example, subshell 1s comprises of one orbital and thus the maximum number of electrons present in 1s subshell can be two, in p and d subshells, the maximum number of electrons can be 6 and 10 and so on. This can be summed up as : the maximum number of electrons in the shell with principal quantum number n is equal to 2n².

Hund’s Rule of Maximum Multiplicity

This rule deals with the filling of electrons into the orbitals belonging to the same subshell (that is, orbitals of equal energy, called degenerate orbitals). It states : pairing of electrons in the orbitals belonging to the same subshell (p, d or f) does not take place until each orbital belonging to that subshell has got one electron each i.e., it is singly occupied.

Since there are three p, five d and seven f orbitals, therefore, the pairing of electrons will start in the p, d and f orbitals with the entry of 4th, 6th and 8th electron, respectively. It has been observed that half filled and fully filled degenerate set of orbitals acquire extra stability due to their symmetry.

Stability of Completely Filled and Half Filled Subshells

The ground state electronic configuration of the atom of an element always corresponds to the state of the lowest total electronic energy. The electronic configurations of most of the atoms follow the basic rules, However, in certain elements such as Cu, or Cr, where the two subshells (4s and 3d) differ slightly in their energies, an electron shifts from a subshell of lower energy (4s) to a subshell of higher energy (3d), provided such a shift results in all orbitals of the subshell of higher energy getting either completely filled or half filled. The valence electronic configurations of Cr and Cu, therefore, are 3d⁵4s¹ and 3d¹⁰ 4s¹ respectively and not 3d⁴ 4s² and 3d⁹ 4s². It has been found that there is extra stability associated with these electronic configurations.

Stability of Completely Filled and Half Filled Subshells

The ground state electronic configuration of the atom of an element always corresponds to the state of the lowest total electronic energy. It has been found that there is extra stability associated with completely filled and half filled electronic configurations because of following reasons: 

1) Symmetrical distribution of electrons:

The completely filled or half filled subshells have symmetrical distribution of electrons in them and are therefore more stable. their shielding of one another is relatively small and the electrons are more strongly attracted by the nucleus.

2. Exchange Energy:

The stabilizing effect arises whenever two or more electrons with the same spin are present in the degenerate orbitals of a subshell. These electrons tend to exchange their positions and the energy released due to this exchange is called exchange energy. The number of exchanges that can take place is maximum when the subshell is either half filled or completely filled As a result the exchange energy is maximum and so is the stability.

We can say that  the extra stability of half-filled and completely filled subshell is due to:

1) relatively small shielding,

2) smaller coulombic repulsion energy, and

3) larger exchange energy.

Details about the exchange energy will be dealt with in higher classes.

Electronic Configuration of Atoms

The distribution of electrons into orbitals of an atom is called its electronic configuration. If one keeps in mind the basic rules which govern the filling of different atomic orbitals, the electronic configurations of different atoms can be written very easily.

The electronic configuration of different atoms can be represented in two ways : 

(i) s^a p^b d^c …… notation

(ii) Orbital diagram

In the first notation, the subshell is represented by the respective letter symbol and the number of electrons present in the subshell is depicted, as the super script, like a, b, c, … etc. The similar subshell represented for different shells is differentiated by writing the principal quantum number before the respective subshell.

In the second notation each orbital of the subshell is represented by a box and the electron is represented by an arrow (↑) a positive spin or an arrow (↓) a negative spin. The advantage of second notation over the first is that it represents all the four quantum numbers.

The electrons in the completely filled shells are known as core electrons and the electrons that are added to the  electronic shell with the highest principal quantum number are called valence electrons. For example, the electrons in Ne are the core electrons and the electrons from Na to Ar are the valence electrons.

We may be puzzled by the fact that chromium and copper have five and ten electrons in 3d orbitals rather than four and nine as their position would have indicated with two-electrons in the 4s orbital. The reason is p³, p⁶, d⁵, d¹⁰, f⁷, f¹⁴ are fully filled orbitals and halffilled orbitals have extra stability.

the electronic configuration is show as:

..........END OF THIS UNIT..........

UNIT 2.4 QUANTUM MECHANICAL MODEL

LEC: 8 TOWARDS QUANTUM MECHANICAL MODEL OF THE ATOM

In view of the shortcoming of the Bohr’s model, attempts were made to develop a more suitable and general model for atoms. Two important developments which contributed significantly in the formulation of such a model were :

1. Dual behaviour of matter,
   
2. Heisenberg uncertainty principle.       

Dual Behaviour of Matter

The French physicist, de Broglie in 1924 proposed that matter, like radiation, should also exhibit dual behaviour i.e., both particle and wavelike properties. This means that just as the photon has momentum as well as wavelength, electrons should also have momentum as well as wavelength, de Broglie gave the following relation between wavelength (λ) and momentum (p) of a material particle.
λ = h/mv =h/p           
where m is the mass of the particle, v its velocity and p its momentum. de Broglie’s prediction was confirmed experimentally when it was found that an electron beam undergoes diffraction, a phenomenon characteristic of waves. The wavelengths associated with ordinary objects are so short (because of their large masses) that their wave properties cannot be detected. The wavelengths associated with electrons and other subatomic particles (with very small mass) can however be detected experimentally. Results obtained from the following problems prove these points qualitatively.

Heisenberg’s Uncertainty Principle

Werner Heisenberg a German physicist in 1927, stated uncertainty principle which is the consequence of dual behaviour of matter and radiation. It states that it is impossible to determine simultaneously, the exact position and exact momentum (or velocity) of an electron. Mathematically, it can be given as in equation   

where Δx is the uncertainty in position and Δp ( or Δv) is the uncertainty in momentum (or velocity) of the particle. If the position of the electron is known with high degree of accuracy (Δx is small), then the velocity of the electron will be uncertain (Δv is large). On the other hand, if the velocity of the electron is known precisely (Δv is small), then the position of the electron will be uncertain (Δx will be large).

now there must be some confusions and some question arises in our minds that are as follow:

Question1: What are difficulties in measurement of the position and velocity?

Answer: in order to determine the position of an electron, we must use a meterstick calibrated in units of smaller than the dimensions of electron (keep in mind that an electron is considered as a point charge and is therefore, dimensionless). To observe an electron, we can illuminate it with ‘light’ or electromagnetic radiation. The ‘light’ used must have a wavelength smaller than the dimensions of an electron. The high momentum photons of such light (p = h/ λ) would change the energy of electrons by collisions. In this process we, no doubt, would be able to calculate the position of the electron, but we would know very little about the velocity of the electron after the collision.

Question 2: what is Significance of Heisenberg’s Uncertainty Principle?

Answer: One of the important implications of the Heisenberg Uncertainty Principle is that it rules out existence of definite paths or trajectories of electrons and other similar particles. The trajectory of an object is determined by its location and velocity at various moments. If we know where a body is at a particular instant and if we also know its velocity and the forces acting on it at that instant, we can tell where the body would be sometime later. We, therefore, conclude that the position of an object and its velocity fix its trajectory. Since for a sub-atomic object such as an electron, it is not possible simultaneously to determine the position and velocity at any given instant to an arbitrary degree of precision, it is not possible to talk of the trajectory of an electron.

Question 3: on which particles Uncertainity priciple is applicable?

Answer: The effect of Heisenberg Uncertainty Principle is significant only for motion of microscopic objects and is negligible for that of macroscopic objects. This can be seen from the following examples.

If uncertainty principle is applied to an macroscopic object of mass10^-6 kg, then

Δv.Δx = h/4π.m = (6.626×10^-34)Js)/(4×3.1416×10^-6 kg) ≈ 10^-28m²s^-1    

The value of ΔvΔx obtained is extremely small and is insignificant. Therefore, one may say that in dealing with milligram-sized or heavier objects, the associated uncertainties are hardly of any real consequence.

In the other case of a microscopic object like an electron of mass is 9.11×10^-31 kg, then

Δv.Δx = h/4π.m = (6.626×10^-34)Js)/(4×3.1416×9.11×10^-31 kg) = 10^-4m²s^-1

means that if we try to find the exact location of the electron to an uncertainty of only 10^-8 m, then the uncertainty  in Δv velocity would be 10^-4m²s^-1/10^-8m ≈ 10⁴m s^-1 which is so large that the classical picture of electrons moving in Bohr’s orbits (fixed) cannot hold good.

RESULT: It, therefore, means that the precise statements of the position and momentum of electrons have to be replaced by the statements of probability, that the electron has at a given position and momentum. This is what happens in the quantum mechanical model of atom.

QUANTUM MECHANICAL MODEL OF ATOM

Classical mechanics, based on Newton’s laws of motion, successfully describes the motion of all macroscopic objects such as a falling stone, orbiting planets etc., which have essentially a particle-like behavior as shown in the previous section. However it fails when applied to microscopic objects like electrons, atoms, molecules etc. This is mainly because of the fact that classical mechanics ignores the concept of dual behavior of matter especially for sub-atomic particles and the uncertainty principle. The branch of science that takes into account this dual behavior of matter is called quantum mechanics. .

Quantum mechanics is a theoretical science that deals with the study of the motions of the microscopic objects that have both observable wave like and particle like properties. It specifies the laws of motion that these objects obey. When quantum mechanics is applied to macroscopic objects (for which wave like properties are insignificant) the results are the same as those from the classical mechanics.

Quantum mechanics was developed independently in 1926 by Werner Heisenberg and Erwin Schrödinger. Here, however, we shall be discussing the quantum mechanics which is based on the ideas of wave motion. The fundamental equation of quantum mechanics was developed by Schrödinger and it won him the Nobel Prize in Physics in 1933. Schrodinger equation is the quantistical equivalent of Newton's law in the sense that while Newton's law tells you the "future story" of a non-quantistical particle (its trajectory due to forces), the Schrodinger equation tells you the same for a quantistical particle. The difference being that for a quantistical particle you cannot speak of a trajectory in the classical sense due to the Heisenberg uncertainty principle, but you can speak of a wave function (with a probabilistic meaning) and Schrodinger equation will tell you the "future story" of the wave function

For a system (such as an atom or a molecule whose energy does not change with time) the Schrödinger equation is written as

The total energy of the system takes into account the kinetic energies of all the sub-atomic particles (electrons, nuclei), attractive potential between the electrons and nuclei and repulsive potential among the electrons and nuclei individually. Solution of this equation gives E and ψ.

Hydrogen Atom and the Schrödinger Equation

1) When Schrödinger equation is solved for hydrogen atom, the solution gives the possible energy levels the electron can occupy and the corresponding wave function(s) (ψ) of the electron associated with each energy level.

2) When an electron is in any energy state, the wave function corresponding to that energy state contains all information about the electron.

3) Wave functions of hydrogen or hydrogen like species with one electron are called atomic orbitals. Such wave functions applicable to one-electron species are called one-electron systems.

4) The probability of finding an electron at a point within an atom is proportional to the |ψ|2 at that point.

5) The quantum mechanical results of the hydrogen atom successfully predict all aspects of the hydrogen atom spectrum including some phenomena that could not be explained by the Bohr model.

6) Application of Schrödinger equation to multi-electron atoms presents a difficulty: the Schrödinger equation cannot be solved exactly for a multi-electron atom. This difficulty can be overcome by using approximate methods or by modern Computers.

Important Features of the Quantum Mechanical Model of Atom

Quantum mechanical model of atom is the picture of the structure of the atom, which emerges from the application of the Schrödinger equation to atoms. The following are the important features of the quantum mechanical model of atom:

1) The energy of electrons in atoms is quantized means can only have certain specific values.

2) The existence of quantized electronic energy levels is a direct solutions of Schrödinger wave equation.

3) Both the exact position and exact velocity of an electron in an atom cannot be determined simultaneously (Heisenberg uncertainty principle). The path of an electron in an atom therefore, can never be determined or known accurately. That is why, we can only talk about the probability of finding  electron at different points in an atom.

4) A wave function for an electron in an atom is called an atomic orbital. Whenever an electron is described by a wave function, we say that the electron occupies that orbital.
Since many such wave functions (atomic orbital) are possible for an electron, In each orbital, the electron has a definite energy. All the information about the electron in an atom is stored in its orbital wave function ψ and quantum mechanics makes it possible to extract this information out of ψ.

5) The probability of finding an electron at a point within an atom is proportional to the square of the orbital wave function i.e., |ψ|² at that point. |ψ|² is known as probability density and is always positive. From the value of |ψ|² at different points within an atom, it is possible to predict the region around the nucleus where electron will most probably be found.

Orbitals and Quantum Numbers

We have already studied that by solving the Schrödinger equation (Hψ = Eψ), we obtain a set of mathematical equations, called wave functions (ψ), which describe the probability of finding electrons at certain energy levels within an atom.

A wave function for an electron in an atom is called an atomic orbital; this atomic orbital describes a region of space in which there is a high probability of finding the electron. Energy changes within an atom are the result of an electron changing from a wave pattern with one energy to a wave pattern with a different energy (usually accompanied by the absorption or emission of a photon of light).

These quantized energy states and corresponding wave functions which are characterized by a set of three quantum numbers principal quantum number n, azimuthal quantum number l and magnetic quantum number ml) arise in the solution of the Schrödinger equation. When an electron is in any energy state, the wave function corresponding to that energy state contains all information about the electron. The wave function is a mathematical function whose value depends upon the coordinates of the electron in the atom and does not carry any physical meaning.

Hence Each electron in an atom is described by four different quantum numbers. The first three (n, l, ml) specify the particular orbital of interest, and the fourth (ms) specifies how many electrons can occupy that orbital. Now lets see all these quantum number in detail

1) Principal Quantum Number (n): 

a) Specifies the energy of an electron and the size of the orbital (the distance from the nucleus),   the larger the number n is, the farther the electrons are from the nucleus, the larger the size of the orbital, and the larger the atom is.
.
b) n can be any positive integer starting at 1, as n=1 designates the first principal shell (the innermost shell). The first principal shell is also called the ground state, or lowest energy state. All orbitals that have the same value of n are said to be in the same shell (level).

c) When an electron is in an excited state or it gains energy, it may jump to the second principle shell, where n=2. This is called absorption because the electron is "absorbing" photons, or energy. Known as emission, electrons can also "emit" energy as they jump to lower principle shells, where n decreases by whole numbers.

d) With the increase in the value of ‘n’, the number of allowed orbital increases and are given by ‘n²’.
e) All the orbitals of a given value of ‘n’ constitute a single shell of atom and are represented by the following letters

n        =     1       2       3       4 ............

Shell  =     K      L       M      N ............

When the value of n is higher, the number of principal electronic shells is greater. This causes a greater distance between the farthest electron and the nucleus. As a result, the size of the atom and its atomic radius increases.

2) Angular Momentum (Secondary / Azimunthal) Quantum Number (l)

a) it Specifies the shape of an orbital with a particular principal quantum number. 

b) Each shell consists of one or more subshells or sub-levels. The number of subshells in a principal shell is equal to the value of n from 0 to n-1.

c) Each sub-shell is assigned an azimuthal quantum number (l ). Sub-shells corresponding to different values of l are represented by the following symbols 

value of  l                       0            1            2            3            4            5          ...

Name of Subshell         s            p            d            f             g            h          ...

the arrangement can be shown as

3) Magnetic orbital quantum number. ‘ml’

a) The magnetic quantum number ml determines the number of orbitals and their orientation within a subshell.

b) its value depends on the orbital angular momentum quantum number l, For any sub-shell (defined by ‘l’ value) 2l+1 number of values of ml are possible and these values are given by

ml = -l, -(l-1), -(l-2)....-1, 0, 1, ....(l-2), (l-1), l

c) hence for a value of ml or subshell we can represent ml and number of orbital as 

4) Electron Spin Quantum Number (ms)

The three quantum numbers labelling an atomic orbital can be used equally well to define its energy, shape and orientation. But all these quantum numbers are not enough to explain the line spectra observed in the case of multi-electron atoms, that is, some of the lines actually occur in doublets (two lines closely spaced), triplets (three lines, closely spaced) etc. This suggests the presence of a few more energy levels than predicted by the three quantum numbers.

In 1925, George Uhlenbeck and Samuel Goudsmit proposed the presence of the fourth quantum number known as the electron spin quantum number (ms). An electron spins around its own axis, much in a similar way as earth spins around its own axis while revolving around the sun. In other words, an electron has, besides charge and mass, intrinsic spin angular quantum number. Spin angular momentum of the electron — a vector quantity, can have two orientations relative to the chosen axis. These two orientations are distinguished by the spin quantum numbers ms which can take the values of +½ or –½. These are called the two spin states of the electron and are normally represented by two arrows, ↑ (spin up) and ↓ (spin down). Two electrons that have different ms values (one +½ and the other –½) are said to have opposite spins. An orbital cannot hold more than two electrons and these two electrons should have opposite spins.